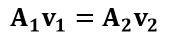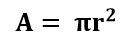Qué es la ecuación de Bernoulli?

La ecuación de Bernoulli es una consecuencia de la ley de conservación de la energía en el flujo de fluidos. Expresión que permite describir el comportamiento de un fluido que se desplaza a lo largo de un tubo de flujo. Dado que esta ecuación es de gran importancia en los estudios de ingeniería, se utiliza para resolver problemas de flujo ideal de forma casi inmediata.

La ecuación de Bernoulli es directamente aplicable a cualquier problema de flujo de fluidos, ya que en la mayoría de los casos es mucho más sencilla que recurrir a complejas ecuaciones diferenciales de momento.

En este artículo explicamos la ecuación de Bernoulli y resolvemos algunos ejemplos utilizando esta ecuación.

Principio de Bernoulli

El principio de Bernoulli es un enunciado bastante especial, ya que parece contradictorio, puesto que plantea una relación entre la velocidad y la presión del fluido sometido a prueba. Este principio establece:

El principio de Bernoulli establece que dentro de un flujo horizontal de fluidos, los puntos de mayor velocidad de dicho fluido deberán tener una presión menor a los puntos que cuentan con una velocidad menor de fluido. 

Esta afirmación explica que cuanto mayor sea la velocidad del fluido en el conducto de trabajo, menor será su presión. También dice que es un fluido horizontal, lo que no debe tomarse literalmente ya que puede haber diferencias de altura y de pendiente ya que la trayectoria del fluido no es siempre horizontal.

Sin embargo, hay que tener en cuenta que el cambio de altura entre los puntos de funcionamiento del fluido no debe ser demasiado pronunciado, porque si lo es, el cambio de energía potencial bajo la gravedad se vuelve significativo, desviándose significativamente del principio de Bernoulli.

En otras palabras, al cambiar el diámetro del tubo a través del cual se mide el fluido bajo prueba, se puede observar un aumento en la velocidad de ese fluido en ciertas partes del tubo. Por otro lado, en las zonas donde el fluido se mueve más rápido, la presión siempre será menor que en las zonas donde el fluido se mueve más lentamente.

Deducción del Principio de Bernoulli

Para entender el principio de Bernoulli, veamos un ejemplo cotidiano de agua que fluye por una manguera bajo presión. El agua es un líquido incompresible, por lo que tiende a aumentar su velocidad si se encuentra en una sección de tubería mucho más pequeña para mantener un volumen de flujo constante, como por ejemplo bajo presión en el extremo de una manguera.

Esta energía cinética ganada por un fluido incompresible (en este caso el agua) se debe a la adición de trabajo externo con el fluido. Esta adición de trabajo puede expresarse como el principio de trabajo-energía de la siguiente manera:

Donde:

• v_f: Velocidad final o del punto final de estudio de fluido
• v_i: Velocidad inicial o del punto inicial de estudio del fluido
• m: Masa del fluido

Cuando un fluido gana energía cinética (su velocidad aumenta), se puede deducir de la ecuación que es el resultado de un trabajo externo sobre ese fluido. Este trabajo se debe a fuerzas externas que provocan un trabajo negativo, pero para entender el principio, consideramos que estas fuerzas viscosas son despreciables y el flujo del fluido es laminar, es decir, fluye en forma regular capas paralelas sin crear un vórtice en el fluido.

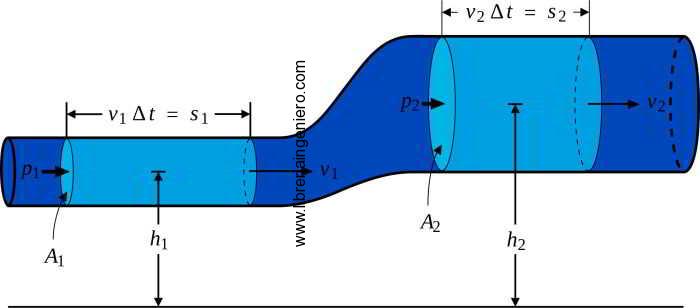
Teniendo en cuenta estas consideraciones, la presión del fluido debe seguir siendo considerada como la causa de los cambios de energía cinética. Para una mejor visión, nos centraremos en la siguiente figura:

En la figura, vemos que el agua fluye de izquierda a derecha a lo largo de la línea de flujo, y la velocidad del fluido aumenta a medida que el diámetro se estrecha. realiza un trabajo positivo a la derecha. Por el contrario, como la fuerza de presión en el punto 2 (P2) es opuesta a la dirección del fluido, realiza un trabajo negativo y empuja el fluido hacia la izquierda.

Debido a la ecuación de continuidad, sabemos que el agua debe acelerarse al salir de la boquilla de la manguera, por lo que se espera un trabajo positivo al salir el fluido de la manguera. Por lo tanto, la presión en el punto 1 debe ser mayor que en el punto 2. En otras palabras, la presión en el lado lento de la manguera (diámetro de tubo mayor) es mayor que en el lado rápido (diámetro de tubo menor). . Esta relación inversa se denomina principio de Bernoulli y confirma así el teorema descrito anteriormente.

Obsérvese que la presión a la que se refiere el principio de Bernoulli es la presión interna que se ejerce en todas las direcciones del fluido cuando éste fluye por el tubo. Esta presión es diferente de la que ejerce el agua cuando sale de una manguera y golpea un objeto con fuerza.

Del mismo modo, el principio de Bernoulli no demuestra que la presión de los fluidos de alta velocidad no pueda ser elevada, sino que se limita a afirmar que la presión de estos fluidos es mucho mayor en las regiones donde su velocidad es menor que en las regiones donde el fluido es de mayor velocidades.

Ecuación de Bernoulli

Esta famosa ecuación es simplemente una expresión matemática del principio de Bernoulli que tiene en cuenta los cambios de energía potencial. A continuación, restamos la ecuación, pero primero hacemos un trabajo para entender y ver cómo se puede utilizar.

La ecuación de Bernoulli apareció en la obra hidrodinámica de Daniel Bernoulli en 1738. Esta ecuación nos ayuda a entender que el flujo ideal (sin viscosidad ni fricción) se refiere a la presión, la velocidad y la altura de dos puntos cualesquiera de un fluido en un sistema laminar de densidad constante. La ecuación de Bernoulli suele escribirse como sigue:

Donde:

• P₁: Presión de fluido en el punto 1
• P₂: Presión del fluido en el punto 2
• v₁: Velocidad del fluido en el punto 1
• v₂: Velocidad del fluido en el punto 2
• h₁: Altura del fluido en el punto 1
• h₂: Altura del fluido en el punto 2
• ρ: Densidad del fluido
• g: Aceleración de gravedad

No olvides que cualquiera de los puntos de prueba puede estar en el tubo. Los puntos marcados en la figura son sólo de referencia y puedes elegir cualquiera para investigar el comportamiento del fluido al utilizar la ecuación de Bernoulli.

La pregunta más habitual que se hacen los alumnos es cómo elegir los puntos a los que aplicar la ecuación de Bernoulli. La respuesta es relativa, y la solución de la ecuación depende de los datos disponibles. Generalmente se considera que este es el segundo punto, el punto en el que tenemos información sobre el fluido a la entrada del manómetro (basado en los datos de presión del fluido) o el punto en el que el fluido está abierto a la atmósfera, ya que en este punto la presión absoluta es la atmosférica .

Obsérvese que se suele tomar como referencia el punto más bajo de la altitud, h = 0. Como puede verse, la ecuación de Bernoulli es el resultado de aplicar la ley de conservación de la energía a un fluido en movimiento.

Deducción de la ecuación de Bernoulli

De forma similar a nuestra conclusión del principio de Bernoulli, explicamos de dónde procede la ecuación de Bernoulli. Para ello, utilice el siguiente formato:

Podemos ver que el fluido se mueve de izquierda a derecha a través de la tubería, así como la diferencia de diámetro y altura. de un punto a otro. Obsérvese también que el diámetro es menor en el segundo punto y (como se ve en la notación de Bernoulli) en este punto la velocidad del fluido será mayor que en el punto de mayor diámetro, para mantener el volumen de flujo a medida que el fluido sube . .

Sin embargo, a medida que el fluido se desplaza hacia arriba, no sólo aumenta la velocidad (energía cinética, K), sino también la energía potencial debida a la gravedad (U). Suponiendo que el fluido no es viscoso, el flujo es laminar y no hay fuerzas disipativas actuando sobre él, podemos decir que cualquier energía introducida en el sistema provoca un trabajo externo sobre el fluido, que puede expresarse como:

En el punto 1 de estudio, el trabajo que se realiza sobre el fluido es positivo, mientras que en el punto 2 es negativo (sentido contrario al movimiento del fluido). Ahora, considerando que W = F x d (fuerza por distancia) y que podemos sustituir F por presión, tendíamos la siguiente expresión:

Donde:

• W: Trabajo.
• P: Presión.
• A: Área de la sección transversal de la tubería.
• d: Desplazamiento de masa de fluido en sección de tubería.

Sustituyendo, para ambos puntos de estudio en la tubería, tenemos la siguiente expresión:

Dado que el volumen de líquido desplazado por el tubo es el mismo y el líquido es incompresible, se concluye que debe desplazarse el mismo volumen de líquido por todos los lados del tubo, por lo que la expresión anterior puede reducirse a:

Tomando en cuenta el cambio de energía cinética y potencial en el sistema estudiado, la ecuación quedaría de la siguiente manera:

Ahora, como el fluido es incompresible la masa desplazada es la misma y el volumen es el mismo. Por lo tanto, agrupando y despejando reducimos la ecuación a:

La segunda es la expresión de la ecuación de Bernoulli, que combina la energía cinética, la energía potencial y la presión entre dos puntos cualesquiera de una tubería.

A menudo se pregunta si la ecuación de Bernoulli es diferente del principio de Bernoulli, y la respuesta es sencilla: sí, aunque ambos están directamente relacionados, el principio de Bernoulli es el resultado de la ecuación de Bernoulli para situaciones en las que la altura del fluido no se modifica de forma significativa.

Ejemplo de uso de la ecuación de Bernoulli

Para entender mejor cómo aplicar la ecuación de Bernoulli a los problemas cotidianos de ingeniería, resolveremos los siguientes ejemplos:

Ejemplo 1.

Se requiere construir una fuente de agua, la cual debe ser alimentada por una tubería cilíndrica de 15 cm de diámetro que transporta agua horizontalmente 8 m bajo el nivel del suelo. La tubería se dobla hacia arriba, disparando el agua por un extremo de tubería de unos 5 cm de diámetro que se localiza a 1.75 m sobre el nivel del suelo. El agua sale a una velocidad de 32 m/s. La densidad del agua es de 1.000 Kg/m3. ¿Cuál será la presión manométrica que requiere la tubería horizontal para esta fuente?.

Resolución

El primer paso para resolver el problema es realizar un gráfico para identificar el sistema que vamos a estudiar.

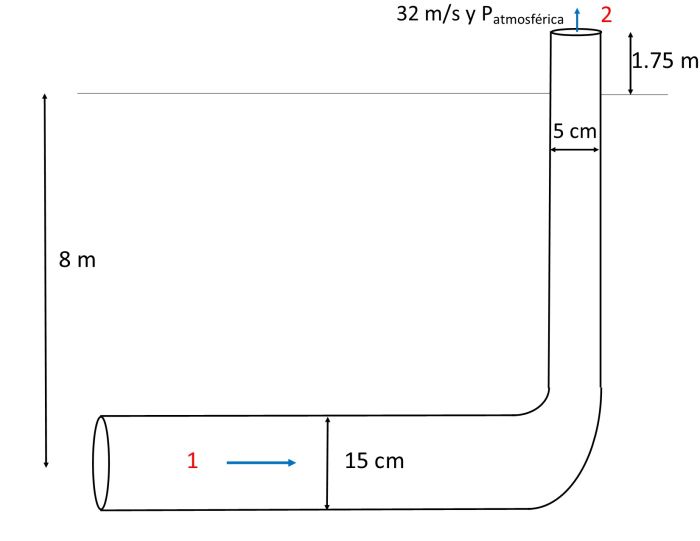
Identificado el sistema y sus variables, es momento de escoger los puntos. Tomamos como punto 1 a cualquier punto del fondo de la tubería (zona horizontal), ya que es allí donde deseamos conocer la presión, y como punto 2, la parte más alta de la tubería, por donde sale el fluido y se encuentra a presión atmosférica, además de conocer la velocidad de salida del fluido en dicho punto.

Con los puntos seleccionados es momento de plantear la ecuación de Bernoulli:

Seguidamente, despejamos la incógnita, que en este caso es la presión en el primer punto P1.

Agrupando términos, la ecuación nos queda de la siguiente manera:

Es momento de identificar los datos, todos conocidos menos v1. Para calcular v1 debemos tener en cuenta la ecuación de continuidad, ya que el agua es un fluido incompresible:

Donde el área de la sección transversal viene dada por:

Sustituyendo, en cada lado de la igualdad y despejando nos queda la siguiente expresión:

Conociendo los radios de cada una de las secciones transversales de los dos puntos y la velocidad de salida del fluido en el punto 2, tenemos:

Conocida la velocidad del fluido en el punto 1, tomamos como referencia h1 = 0. Seguidamente, resolvemos cada uno de los términos de la ecuación de Bernoulli.

Empezaremos con el término relacionado con la velocidad (energía cinética):

Seguimos con el término relacionado con la energía potencial:

Es momento de colocar el término de la presión en el punto 2. Como en dicho punto la presión es atmosférica y deseamos calcular la presión manométrica en el punto uno, vamos a sustituir P2 = 0, ya que la presión manométrica mide presiones por encima de la presión atmosférica. También, se puede sustituir la presión absoluta, recordando restarla cuando calculemos la presión del punto 1 y no errar el resultado. Con todos los términos, sustituimos, quedando lo siguiente:

El resultado del ejemplo 1 es: 

Ejemplo 2

Tomando en cuenta la siguiente figura:

Calcular:

Sustituyendo los valores, tenemos:

Reordenando, tenemos:

Despejando la velocidad del punto F, tenemos:

El resultado para la pregunta a) es: v_F = 7.6720 m/s

Seguidamente, calculamos la presión en el punto B dentro de la tubería. Para ello, la ecuación de Bernoulli se va a realizar entre los puntos A y B, ya que el punto A simplifica bastante los cálculos:

Al estar a la misma altura, la referencia es h=0 para ambos puntos, de modo, que la ecuación queda de la siguiente manera:

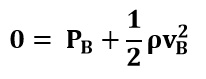
Tomando en cuenta la ecuación de continuidad, tenemos:

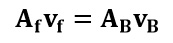
También sabemos que:

Sustituyendo y despejando, tenemos que:

Calculando la presión tenemos:

El resultado para la pregunta b) es: P_B = -4.4925 KPa

A continuación, calculamos la presión en el punto C, el cual es el punto más alto del sistema. Para simplificar los cálculos vamos a tomar la ecuación de Bernoulli entre los puntos A y C, teniendo el siguiente resultado:

Tomando como referencia hA = 0, la ecuación queda simplificada de la siguiente manera:

Necesitamos conocer el valor de la velocidad del fluido en el punto C para poder calcular la presión en dicho punto, para lo cual, vamos a recurrir a la ecuación de continuidad:

Resolviendo, tenemos:

Podemos notar que es la misma velocidad del punto B, ya que la tubería conserva el mismo diámetro. Despejando y sustituyendo, tenemos:

El resultado para la pregunta c) es: P_C = -16.2645 KPa

Para el punto D, el resultado será el mismo que para el punto B, ya que se encuentran a la misma altura y la tubería no sufre cambio de diámetro. Por lo tanto, el resultado para la pregunta d) es: P_D = -4.4925 KPa

Por último, trabajaremos en el punto E. Para ello, vamos a tomar la ecuación de Bernoulli entre los puntos A y E para simplificar los cálculos. Inicialmente, tenemos:

Simplificando la ecuación con los datos tenemos:

La velocidad de E es la misma velocidad de B. Sustituyendo los valores, tenemos:

Despejando, tenemos:

El resultado para la pregunta e) es: P_E = 24.9375 KPa

Como hemos visto, utilizar la ecuación de Bernoulli es bastante sencillo, es importante tener en cuenta la elección de los puntos apropiados para trabajar y, por supuesto, la ecuación de continuidad.