Análisis Granulométrico por Tamizado – Excel

En esta práctica de laboratorio se determina cuantitativamente la distribución de los diferentes tamaños de las partículas que componen a un suelo. Este análisis se aplica a partículas inferiores a 3” y mayores al tamiz Nº 200 (0,075 mm), o a la fracción de suelo compuesta por arenas y gravas.

También permite separar por tamaños las partículas que las componen determinando en porcentaje del peso total, la cantidad de granos de los distintos tamaños que contiene dicho suelo.

El análisis granulométrico por tamizado se realiza para las partículas gruesas comprendidas por gravas y arenas.

El tamaño de partícula en d (mm), se define como la apertura del tamiz de malla cuadrada, por donde pasa el diámetro menor de la partícula. Por ejemplo, el tamiz Nº 200, el número 200 designa la cantidad de aberturas por pulgada de longitud de la malla del tamiz.

El juego de tamices de malla cuadrada que permiten un espaciamiento uniforme en la curva granulométrica es el siguiente:

Coeficiente de Uniformidad (Cu) o de Hazen

Es la relación que existe entre el diámetro que corresponde al 60% de peso más finos y el 10% del mismo. Este coeficiente indica la pendiente media de la curva granulométrica en su parte central.

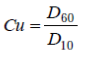
Asimismo, el coeficiente de uniformidad indica la proporción de partículas del mismo tamaño. Por ejemplo: si las partículas son del mismo diámetro Cu=1. «Cu» puede ser un número mayor que uno y el aumento de Cu representa un amplio rango de diferentes tamaños de partícula.

Coeficiente de Curvatura (Cc)

Es la relación del diámetro de porcentaje 30% entre el producto del 60% y 10%.

donde:

D60 = Diámetro en milímetro que cumpla que el 60% del material tenga un tamaño igual o inferior a él.
D30 = Diámetro en milímetro que cumpla que el 30% del material tenga un tamaño igual o inferior a él.
D10 = Diámetro en milímetro que cumpla que el 10% del material tenga un tamaño igual o inferior a él.

El coeficiente de curvatura describe la suavidad y la forma de la curva de gradación. Valores de Cc muy altos o muy bajos indican que la curva es irregular.

El tamaño efectivo es el tamaño máximo de los granos que forman el 10% en peso más fino. (D10 =tamaño o diámetro efectivo)

Realización del Ensayo en el Laboratorio

En el laboratorio el ensayo se realiza por vía húmeda o por vía seca.

La vía húmeda se utiliza cuando el suelo presenta mayor proporción de fino y se realiza lavando la muestra a estudiar por el tamiz número 200.

La vía seca se utiliza cuando el suelo a estudiar predomina material grueso (gravas y arenas) y se realiza haciendo directamente la granulometría con la tamizadora ordenando los tamices de mayor a menor tamaño.

Los pasos a seguir son:

• Si se realiza por vía húmeda o seca se debe determinar el peso total de la muestra PTM.
• Se lava la muestra por el tamiz número 200, permitiendo lavar los finos del suelo a estudiar (vía humeda).
• Se seca la muestra en el horno.
• Se coloca la muestra en la serie de tamices desde el número 3” hasta el Nº4, se puede agitar manualmente

• La muestra pasante por el tamiz número cuatro (Nº 4) se coloca en la serie de tamices desde el numero 10 al número 200 y se agita con la tamizadora.

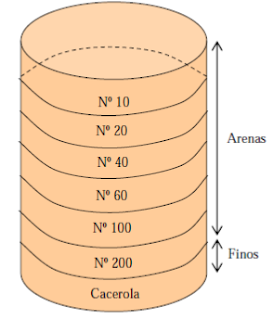
• Luego se determina el peso retenido en cada tamiz: Wret C/T (gr).
• El porcentaje parcial se determina dividiendo el peso retenido en cada tamiz entre el peso total de la muestra: 
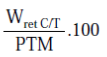
• Luego se determina el porcentaje retenido acumulado, sumando sucesivamente el peso retenido parcial de cada tamiz.
• Por último, se determina el porcentaje pasante, restando 100 menos el porcentaje retenido acumulado.

Curva Granulométrica

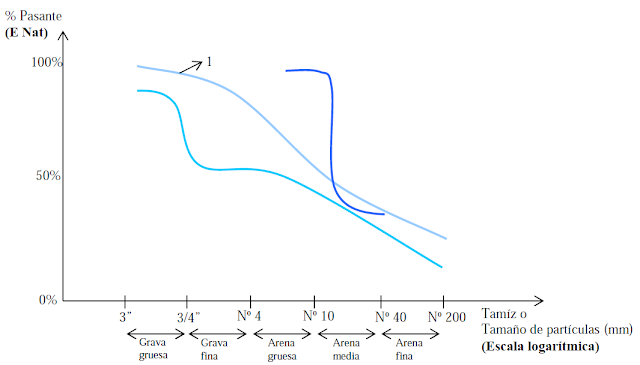
Se tienen suelos bien gradados: cuando la muestra contiene partículas de todos los tamaños y en las mismas proporciones. Por ejemplo, la curva 1.

Los suelos bien gradados deben cumplir:

• El coeficiente de curvatura debe estar entre 1 y 3 —> 1 ≤ Cc ≤ 3
• El coeficiente de uniformidad debe estar: Gravas > 4 y Arenas > 6.

Los suelos mal gradados: presentan ausencia de algunos tamaños o son uniformes, por ejemplo curva 2 presenta ausencia de tamaño de partícula. Y la curva 3 presenta uniformidad en la curva.